
2023-03-09 17:10:05 来源:中公社区工作者考试网 曾佳佳
行测数量关系中的排列组合是公职考试的常见知识点,但是很多考生却在这里丢分,主要原因就是排列组合的考查内容较多,变化形式比较多样。今天中公教育就排列组合中一个特殊而又容易拿分的知识点——隔板模型来进行讲解。
当把n个相同元素分给m个不同的对象,每个对象至少1个元素,问有多少种不同的分法的问题。
三个必要条件:一是分配的n个元素相同;二是分配对象不同;三是每个分配的对象至少分到一个元素。
题目满足以上三个条件,我们就可以用隔板法来解题。
例:20个大小相同的气球,现在需要分配给甲、乙、丙、丁、戊五个小朋友,每个小朋友至少分得一个气球,一共有多少种不同分法?(满足隔板模型三个条件:一、20个气球相同;二、分给五个不同的小朋友;三、每个小朋友至少分一个)
基本公式: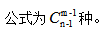
注释:n个元素代表有n-1个位置可以放隔板,分成m份需要放m-1块隔板。
有15个相同的苹果,分给四个小朋友,每个小朋友至少分一个苹果,有( )种不同的分法。
A.364 B.360 C.1365 D.1360
【答案】A。中公解析:题目15个苹果相同,4个小朋友不同,每个小朋友至少一个,满足隔板法题型特征;15个苹果有15-1个位置放置隔板,分成4份需要4-1块隔板。直接使用公式有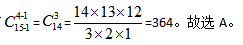
有30个优秀学生奖名额需要分配到编号为1、2、3、4、5的五个班级,每个班级分配的名额数不得少于其编号数。问一共有多少种不同的分配方式?
A.1260 B.780 C.3876 D.4600
【答案】C。中公解析:由题意得出,现每个班级分配的名额数不得少于其编号数,编号不一样。若想使用隔板法,需要把分配名额数转化为“每个班级至少一个”,先给编号1、2、3、4、5的班级分别0、1、2、3、4个名额之后,每个班级至少再分配一个名额,现在题干转化成了标准的隔板模型。现还剩 30-1-2-3-4=20个名额,则可使用隔板法解题,20个名额有20-1个空格可以插入隔板,分成5份需要5-1块隔板,直接使用公式有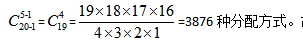 故选C。
故选C。
通过以上的讲解,中公教育相信大家对于隔板模型的题目应该就没有那么困惑了。那最主要就是对于不同类型的题目,要学会去寻找其中的共同点,不断地总结出方法,多多练习以后就可以在较短时间内求解出答案。

 京公网安备 11010802029861号 出版物经营许可证新出发京批字第直130052号
京公网安备 11010802029861号 出版物经营许可证新出发京批字第直130052号
