公益岗行测复习：公约数与公倍数的应用

【导语】行测是公益性岗位考试中很重要的一门，做题当中需要运用很多技巧。当你掌握了技巧后，公益岗行测的题目也就没有想象中的那么难了。中公教育公益岗考试网为大家梳理了一些做题技巧，希望可以帮助考生有所提升。

点击加入公益性岗位考试交流群 744173032 与大家一起交流

微信搜索：gygoffcn 及时关注公益岗考试信息

一、定义

公约数：几个自然数公有的约数，叫做这几个自然数的公约数。

最大公约数：公约数中最大的一个称为这几个自然数的最大公约数。

公倍数：几个自然数公有的倍数。

最小公倍数：公倍数中最小的一个大于零的公倍数。

求解方法1——短除法(如下图所示)

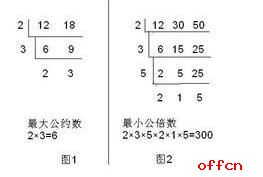
比如12和18的最大公约数就是6;12、30、50的最小公倍数是300

求解方法2——分解质因数法

把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数。例如:求24和60的最大公约数，先分解质因数，得24=2×2×2×3，60=2×2×3×5，24与60的全部公有的质因数是2、2、3，它们的积是2×2×3=12;把所有出现的因数的最高次幂取出来连乘，所得的积就是这几个数的最小公倍数。例如24和60的最小公倍数就是2×2×2×3×5=120。

二、例题精讲

【例1】用一张长1007毫米、宽371毫米的长方形纸，剪成多个面积相等且尽可能大的正方形。长方形纸最后没有剩余，则这些正方形的边长是( )毫米。

A.19 B.53 C.79 D.106

【思路点拨】由“用一张长1007毫米、宽371毫米的长方形纸，剪成多个面积相等且尽可能大的正方形。长方形纸最后没有剩余”可以看出利用最大公约数来解题。

【答案】B。中公解析：要使长方形纸没有剩余，且剪成面积相等且尽可能大的正方形，则正方形的边长应为1007、371的最大公约数，利用短除法求解1007与371的的最大公约数为53毫米。故选B。

【例2】A、B、C、D四人去羽毛球馆打球，A每6天去一次，B每12天去一次，C每18天去一次，D每30天去一次。5月18日，四个人恰好在羽毛球馆相遇，则下一次相遇的时间为( )

A.9月18日 B.10月14日 C.11月14日 D.12月18日

【思路点拨】由“A每6天去一次，B每12天去一次，C每18天去一次，D每30天去一次”，可知要求出6、12、18、30的最小公倍数，然后利用最小公倍数解题。

【答案】C。中公解析：从题意可知，A、B、C、D四人分别每6、12、18、30天去一次羽毛球馆，则他们下一次相遇，需经过的天数是6、12、18、30的最小公倍数，即为180天，180=(31-18)+30+31+31+30+31+14，故5月18日之后的180天是11月14日。