公益性岗位考试内容-行测：“鸡兔同笼”数清楚

鸡兔同笼问题一直以来都是大家非常熟悉的题型，从小学开始就有接触的，在公职类考试行测中，鸡兔同笼问题也是会涉及到的题型之一。接下来，中公教育专家跟大家一起分享鸡兔同笼问题的解题方法。

例：鸡和兔放在同一个笼子里，数头一共35个，数脚一共94只，问笼子中鸡和兔各有多少只?

中公解析：方法一：方程法。比较基础的方法，设笼子当中有鸡x只，兔y只。题干中存在两个等量关系式，第一个是头总共35个，第二个是脚总共94个。可列得方程：

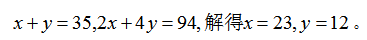
方程法相对来讲好理解一些，但是有的时候方程法解方程的计算量更大一些，而假设法的计算量更小一些。

鸡兔同笼的题型特征：一、题干一般会涉及两个对象：鸡和兔;二、题干中会有两个总量：头35个，脚94个;三、题干中会有两个单量：一只鸡2个脚，一只兔子4个脚。解题原则：设鸡求兔，设兔求鸡。假设全都是鸡，最后求出来的是兔子的数量，假设全都是兔子，最后求出的是鸡的数量。

例：有一辆货车运输2000只玻璃瓶，运费按到达时完好瓶子数目计算，每只2角，如有破损，破损一只还要倒赔2角，结果得到运费393.2元，破损只数是：

A.17 B.24 C.34 D.36

中公解析：首先识别考点：两个对象分别是好的玻璃和破损的玻璃;两个总量分别是2000只玻璃瓶，393.2元也就是3932角;两个单量分别是一只好的玻璃瓶2角，一只破损的玻璃瓶倒赔两角。假设都是好的玻璃瓶，总价应该是4000角，实际是3932角，损失了68角，一只好的玻璃瓶如果破损，倒赔2角也就是相当于损失4角，故总共损失了

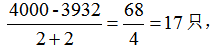
故选择A。

以上就是鸡兔同笼问题的解题方法，可以通过多加练习来提高做题的速度和敏感度。