公益性岗位考试内容-行测：只要特值用的好，工程问题没烦恼

工程问题是每年国考都会出现的题目，这个知识点说难也不难，只要学会了方法，很容易拿到分数。今天，中公教育专家就带大家一起来巧解工程问题。

一、了解工程

在国考中，工程问题的身影始终都在，近10年中出现了11次，每次出现都很容易被辨认出来，使用的解题技巧也很专一，足见它的重要性和简单性。

出题方式：做一项工作，与效率相关，比如挖隧道、制作花朵、割麦子、工程队施工等。

解题技巧：特值法——设工作总量或者工作效率为特值

二、巧用特值

接下来，我们就来看两道国考历年试题感受一下特值法怎么运用：

【例1】工厂有5条效率不同的生产线。某个生产项目如果任选3条生产线一起加工，最快需要6天整，最慢需要12天整;5条生产线一起加工，则需要5天整。问如果所有生产线的产能都扩大一倍，任选2条生产线一起加工最多需要多少天完成?

A.11 B.13 C.15 D.30

【题型判断】生产线上做一项工作，并且每条生产线效率不一。

【解题技巧】特值法，在工程问题基本公式：工作总量=工作效率×工作时间中，题干只知时间，求时间，则公式可以变形成：工作时间=工作总量/工作效率，但工作效率和工作总量都未知，所以我门只要保证二者的相对比例不变即可，那么就满足了特值法的应用环境。其实工作总量和工作效率均可设特值，但是我们发现，设效率的话，量比较多，还不容易满足条件，所以一般做同一项工作的时候，给了工作时间，我们选择去设这个不变的工作总量为特值，一般为时间的最小公倍数。

【中公解析】设工作总量为60，并假定5条生产线的效率从大到小分别为a、b、c、d、e

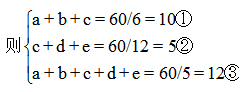
要使加工时间最多，选最慢的两条就可以了，即选择d和e,

根据上述关于效率的式子可得d+e=③-①=12-10=2,

效率提高一倍后为4，则最慢的工作时间为60/4=15.

答案选C。

【例2】某商铺甲乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时，乙组单独制作需要15小时，现两组一起做，期间乙组休息了1小时40分，完成时甲组比乙组多做300朵。问这批花有多少朵?

A.600 B.900 C.1350 D.1500

【题型判断】商铺制作花朵，属于做一项工作，并且每组员工制作效率不一。

【解题技巧】特值法，还记得我门上边的结论吧，一般做同一项工作的时候，给了工作时间，我们选择去设这个不变的工作总量为特值，一般为时间的最小公倍数。

【中公解析】设工作总量为30份，则甲组员工的效率为3，乙组员工的效率为2，期间乙休息的时候甲继续在做，所以可知甲单独做了1小时40分钟即

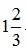
小时，所做的工作量为

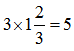
份，还剩30-5=25份是甲乙一起做的，耗时25/(2+3)=5小时，综上，甲共做5+3×5=20份，乙做30-20=10份，甲比乙多做20-10=10份，正好对应的是300朵花，那么一份对应的是30朵，则总量的30份对应的是900朵，故答案选B。

可见只要掌握好特值法，工程问题迎刃而解，快再去找找工程问题练练吧。