公益岗行测技巧：“韩信点兵”问题破解大法（2）

3.差同减差

若两个除式的被除数相同，除数和余数的差也相同，那么这个被除数的值等于两个除数的最小公倍数减去“除数和余数的差”。如：X÷3余2，X÷4余3，那么X=12k-1。

例3.有一个小于200的正整数m，它除以11余8，除以13余10，则2m-80=( )

A.158 B.200 C.226 D. 244

【答案】B。

【中公解析】两个除式的被除数相同，均为m，两式“除数与余数的差”均为3，而除数11、13的最小公倍数是143，根据差同减差可得，m=143k-3。由题可知0

(二)一般情况

三种特殊模型有固定的公式，而对于不符合特殊模型的一般情况，我们则需要利用同余特性构建中间数分步来满足题干条件，进而求得正确答案。

例4：某个正整数P除以3余2，除以7余3，除以11余4，求这个数的最小值。

【中公解析】分析题干发现，三个除式不具备特殊模型的特征，为了逐步满足题干条件求解答案，可以构造A、B、C三个中间数如下表：

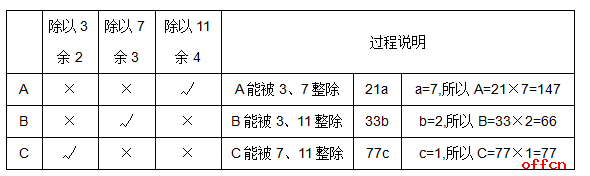
由表可知，A+B+C=21a+33b+77c=147+66+77=290就是满足3个条件的数。由于3、7、11最小公倍数是231，所以P=231k+290。当k取-1时，P取到最小值59。

通过上面“剩余问题”解题方法的学习，我们再回头来思考“韩信点兵”的奥妙，就会豁然开朗。